| Two Minute Puzzles
|
The Parking Lot:
What is the number of the parking space containing the car? (Please hit the picture for a larger version.)

|
Hints: You either see it or you don't.
For the solution, please hit the puzzle name again.
|
|
|
Solution: Flip the screen: 87.
|
|
|
|
Cheryl's Birthday:
Albert and Bernard just became friends with Cheryl, and they want to know when her birthday is. Cheryl gives them 10 possible dates: May 15, May 16, May 19, June 17, June 18, July 14, July 16, August 14, August 15, August 17. Cheryl tells Albert the month, and Bernard the day. First Albert says: "I don't know Cheryl's birthday, but Bernard does not know as well!". Bernard then says: "Now I know Cheryl's birthday, and so does Albert!". When is her birthday?
|
Hints: Drawing a grid with the relevant months and dates might help.
For the solution, please hit the puzzle name again.
|
|
|
Solution: July 16. If Bernard got the number 18 or 19, he would know Cheryl's birthday immediately. So Albert can only be sure that Bernard does not know initially, if Cheryl's birthday is neither in May nor in June. So the birthday must be in July or August. If the day was 14, then Bernard would still not know. So the day must be either 15 (August), 16 (July), or 17 (August). If it was in August, then Albert would still not know (since there are still two possible dates in August). Since Albert now knows as well, it must be July 16.
|
|
|
|
Forty-five Minutes:
How do we measure forty-five minutes using two wires, each of which takes an hour to burn. Unfortunately, the wires burn non-uniformly (sometimes faster, sometimes slower). We have plenty of matchsticks.
|
Hints: No hints.
For the solution, please hit the puzzle name again.
|
|
|
Solution: Light three out of four ends. When two ends meet, light the fourth.
|
|
|
|
The Blind Man:
A blind man was handed a deck of 52 cards with exactly 10 cards facing up. How can he divide it into two piles, each of which having the same number of cards facing up?
|
Hints: No hints.
For the solution, please hit the puzzle name again.
|
|
|
Solution: He removes 10 cards from the pile and flips them. Then he has two piles, each of which having the same number of cards facing up.
|
|
|
|
The Rope:
You are trapped atop a 200m high building. You have a rope 150m long, plus a Swiss Army knife. There is a hook at the top where you stand. Looking down, at midway between you and the ground, at a height of 100m, there is a ledge with another hook. Is it possible to get down safely?
|
Hints: No hints.
For the solution, please hit the puzzle name again.
|
|
|
Solution: Cut rope into 50m and 100m pieces. Tie one end of the 50m piece to the top hook and make a noose at the other end. Pass the 100m piece through the noose and tie its two ends.
|
|
|
|
Duck and Fox:
A duck swims in a perfectly circular pond. There is a fox at the shore, afraid of water, that plans to catch the duck when getting out. The land speed of the fox is four times as high as the water speed of the duck, however, once the duck reaches the shore without the fox in its immediate neighborhood, it can hide and escape. Can the duck reach the shore safely?
|
Hints: No hints.
For the solution, please hit the puzzle name again.
|
|
|
Solution: Yes, the duck can reach the shore! Assume that the pond has radius r. While the duck is strictly within radius r/4 of the center of the pond, it is radially faster than the fox. In other words, while staying in this small radius the duck can reach the "opposite side" of the fox. Once the duck reaches that opposite point, it will swim straight to the shore. The remaining distance is 3r/4. The fox on the other hand has a distance of pi*r, for which he needs pi*r/4 time. Since 3 < pi the duck wins. (Well, not in Indiana in 1897.)
If you wonder how much faster the fox may be, so that the duck will still reach the shore: the answer to that is about 4.603.
|
|
|
|
The Triangles:
Both "triangles" are made of exactly the same pieces. So where is the gap in the lower triangle coming from?! (Please hit the picture for a larger version.)
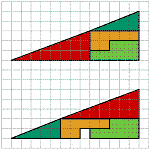
|
Hints: No hints.
For the solution, please hit the puzzle name again.
|
|
|
Solution: There is a "break" where the red and the dark green pieces meet. The lower triangle is "convex" whereas the upper is "concave".
|
|
|
|
99 Cops:
A town has 99 cops. A cop is either honest or corrupt, the majority of the cops is honest. You need to figure out all the corrupt cops, with less than 299 questions. All cops know who is honest and who is corrupt, but only honest cops will answer truthfully. Corrupt cops may lie arbitrarily. For security reasons you can only ask one type of question: You may ask cop X whether cop Y is corrupt. This question will by answered by X with either "Y is corrupt" or "Y is honest".
|
Hints: Consider less cops, e.g. 3 (of which at most one is corrupt) or 16 (at least 9 are honest).
For the solution, please hit the puzzle name again.
|
|
|
Solution: Pair the cops arbitrarily. If the number of cops is odd, the last cop is a singleton. For each pair, ask both cops about the other cop.
If at least one cop calls the partner cop corrupt, discard both cops. If both cops attest the other to be honest, keep one of them, discard the other (arbitrarily).
If the number of cops kept in a round is even, keep the singleton cop as well. If the number of cops is odd, discard the singleton cop. Continue as long as you have more than one cop!
We will prove below that this last cop is honest. All you need to do is to ask this honest cop about all the others, and you will know all honest cops.
Why does this work? Initially we have strictly less corrupt (C) than honest (H) cops, that is C < H. Assume that the number of cops is even.
After pairing, we remove all the HC pairs because at least the honest cop will say that the other cop is corrupt. So we are left with HH and CC pairs, with CC < HH.
Since we keep only one cop per pair, we still have C < H. Thanks to keeping/discarding the singleton cop this is also true if we have an odd number of cops:
In case the singleton is corrupt, the pairs alone will guarantee C < H. In case the singleton is honest, he will break the tie if needed. No matter what, after every round we have C < H.
Also, in each round cops are discarded, so eventually we end up with one cop only; thanks to our induction C < H the remaining cop is honest. For all that we need less than 299 questions.
Thanks to the recursion we discard half of the cops each round. A closer analysis with the rounding because of singletons reveals that we no more than 98+48+24+12+6+2+98 = 288 questions.
Some have pointed out that other strategies are more efficient. The most efficient solution I have received so far is by Varsha Dani, using at most 147 questions, or in general, with n copy, n odd, 3(n-1)/2 questions.
|
|
|
|
|
|
| That's impossible! Or is it?!?
|
Two Cards:
You have to play a series of 1000 games against an opponent, and win at least 501 of them. In each game, the opponent chooses two carefully selected cards from the 13 hearts cards from the deck, from 2 up to ace.
You can sample one of the two cards, and must then decide whether the still hidden card is higher than the card that was revealed. If you are right, you win the game. How can you make (almost) sure to win 501 out of 1000 games?
|
Hints: As always, you should first think about a simplified version of the game. If the deck had only 2 cards, the game is trivial. What about 3, 4, ...?
For the solution, please hit the puzzle name again.
|
|
|
Solution: Contrary to intuition, a player can gain an advantage in this game. To simplify our explanations, we assign the numbers 11 to 14 to the cards jack, queen, king and ace, so the original hearts-only deck consists of the cards 2 to 14. Here is a winning strategy: The player randomly inspects c, one of the two adversarial cards. Then the player chooses a random value r out of {2.5,3.5,4.5,5.5,6.5,7.5,8.5,9.5,10.5,11.5,12.5,13.5}. You may think of this random choice as drawing a random card from a deck of diamond cards only, without the ace, adding 1/2 of the chosen card. If r > c, you bet that the still hidden card is higher. If r < c, you stop and bet on the already seen card to be higher.
It's simple to see that this works: If r is smaller (or larger) than both cards, the probability that the randomly inspected card c was the larger of the two cards is exactly 50%. However, if the randomly chosen value r is between the two cards, you win for sure! Since you choose r in between any two cards with probability at least 1/12, we get a total winning probability of at least 13/24 > 54%.
Plugging this into the binomial formula will reveal that your chance of winning at least 501 games in the series is more than 99.5%.
|
|
|
|
12 Men:
In episode 18 of season 2 of TV show Brooklyn Nine-Nine, Captain Ray Holt challenges his crew with the following puzzle: There are twelve men on an island, eleven weigh exactly the same amount, but one of them is slightly lighter or heavier, you must figure out which. The island has no scales, but there is a see-saw. The exciting catch: You can only use it three times.
|
Hints: A see-saw can give you more than just a single bit of information, since both sides of the see-saw may be equally heavy. So using the see-saw three times gives you 3*3*3 = 27 possible outcomes. One can even tell whether the odd man is heavier or lighter, however this is not needed for the simple Brooklyin Nine-Nine version of this puzzle.
For the solution, please hit the puzzle name again.
|
|
|
Solution: Let's first weigh 4 arbitrary men (group A) against 4 other arbitrary men (group B).
If group A is heavier than group B we know that either group A features a heavy man, or group B a light man, we are left with 8 possibilities.
We use the see-saw a second time, with two men from group A and one from group B on each side.
Say the left side is heavier, then we know that either one of the two As on the left is heavier, or the B of the right is lighter.
So for the third see-saw usage we just measure the two A's from the left.
If one is heavier than the other, he is the odd man. If they are the same, it was B from the right.
If AAB on the left is equally heavy as AAB on the right, we know that one of the two Bs that we did not measure in the second round must be lighter, and we can simply measure them to figure out the odd man.
The case where group B is heavier in the first measurement is equivalent.
If however group A and group B are the same weight, the odd man must be from the remaining 4 men (of group C).
In this case all the men in groups A and B are normal weight.
We use the see-saw simply by measuring two men from group C against two normal-weight men, e.g. from group A.
If CC is heavier (lighter) than AA we know that one of the CCs must be heavy (light) and we figure out which by measuring these two with the see-saw.
If CC is equal to AA, we know that the suspect is one of the two not yet measured men from C. We simply measure one of them with any already measured normal-weight guy and directly know whether he (or the other) is the odd man.
|
|
|
|
Four Cards:
You have to win a game against an opponent. Before the game starts you are blindfolded. There are four cards placed on a square table, one card at each corner. The initial configuration of the cards is chosen by the opponent, arbitrarily and unknown to you. Your goal is to have all four cards face up. In each move you can select any subsets of the four cards, which are then flipped simultaneously by the opponent. After your move, if all four cards are face up, you win. If not, the opponent may rotate the table by an amount of his choice (90, 180, 270, or 360 degrees). If you don't manage to have all four cards face up in 20 moves or less, you lose. What's your strategy?
|
Hints: As always, you should first think about a simplified version of the game. In this case the simple version has only two cards, on opposite sides of a stick; the opponent may or may not turn the stick.
For the solution, please hit the puzzle name again.
|
|
|
Solution: The solution for the two-card came is simple. First turn both cards, then turn one card (which does not matter), then turn both cards.
For four cards the problem is a bit more intricate. Indeed you have to distinguish four configurations:
- FOUR: all four cards are face down;
- OPPOSITE: two cards in opposite corners are face down, the two other cards (also in opposite corners) are face up;
- TWO: two cards on one half of the table are face down, the two other cards on the other half are face up;
- SINGLE: A single card is different from the three other cards.
These four states have increasing difficulty. If the initial configuration was FOUR we are done by just flipping all cards (we call this move 'F'). If the initial configuration was OPPOSITE we get to the FOUR state by flipping two (any two) opposite cards (move 'O'). From there we again win by flipping all four cards. If the initial configuration was TWO we get to FOUR or OPPOSITE by flipping any two cards in sequence (move 'T'). Finally, if the initial configuration is SINGLE we can get to some other configuration by just flipping any single card (move 'S'). In other words, the deterministic winning strategy is: F, O, F, T, F, O, F, S, F, O, F, T, F, O, F. Independent of the initial configuration these 15 moves win, even if the opponent knows our strategy.
|
|
|
|
100 Hats:
To be released from prison, 100 prisoners have to win a game against the hangman. The hangman gives a hat to every prisoner, the hat shows a two-digit integer number between 00 and 99. The numbers do not have to be different, the hangman can also choose to give each prisoner a hat with the same number. Prisoners can see the numbers on the other hats, but they cannot see their own number. Before playing the game, prisoners can discuss their strategy, but once the game starts there is an absolute communication stop. Now each prisoner has to guess his number. If any prisoner guesses his number correctly, all prisoners are released. If no prisoner guesses right, the hangman executes his job. What's the strategy?
|
Hints: As always, you should first think about a simplified version of the game, with only two prisoners (and the possible numbers 1 and 2).
For the solution, please hit the puzzle name again.
|
|
|
Solution: With only two prisoners the solution is simple, prisoner A just guesses the number he saw on B's hat, prisoner B guesses the number not on A's hat. If the hangman gave both prisoners the same number, prisoner A will guess right. In the other case, prisoner B guesses right.
The solution for n players is more or less the natural generalization. The idea is that prisoner k (for k from 0 to n-1) is responsible to report the correct result if the sum of all hats modulo n is equal to k. Consequentially prisoner k reports k minus the sum of the numbers on the other n-1 hats, modulo n.
Example: We have 100 prisoners, and assume that the sum of all hats is 5678. So what about prisoner 78? Assume that there is a 17 on their hat, because the total sum is 5678, prisoner 78 sees a sum of 5661 on the other hats. The subtracts the numbers, divides the result by 100, and takes the remainder, which happens to be 17.
|
|
|
|
The Switch:
The hangman summons his 100 prisoners, announcing that they may meet to plan a strategy, but will then be put in isolated cells, with no communication.
He explains that he has set up a switch room which contains a single switch, which is either on or off.
It is not known to the prisoners whether the switch initially is on or off.
Also, the switch is not connected to anything, but a prisoner entering the room may see whether the switch is on or off (because the switch is up or down). Every once in a while, the hangman will let one arbitrary prisoner into the switch room.
The prisoner may throw the switch (on to off, or vice versa), or leave the switch unchanged. Nobody but the prisoners will ever enter the switch room.
The hangman promises to let any prisoner enter the room from time to time, arbitrarily often.
That is, eventually, each prisoner has been in the room at least once, twice, a thousand times, any number you want.
At any time, any prisoner may declare "We have all visited the switch room at least once". If the claim is correct, all prisoners will be released.
If the claim is wrong, the hangman will execute his job (on all the prisoners). What's the strategy?
|
Hints: As always, you should first think about a simplified version of the game. Assume for instance that the switch is initially off. What's a strategy with two prisoners only? Three? What if one of the prisoners is a leader?
For the solution, please hit the puzzle name again.
|
|
|
Solution: Assume that the switch is initially off. One prisoner is the leader. The leader will turn the switch on whenever possible, that is, whenever the switch is off.
Any other prisoner will (if possible) turn the switch off, but only the first time it encounters a switch that is on. In other words, the second time a prisoner finds the switch on, the prisoner will leave it on.
The leader will (if possible) throw the switch on. After having done that 100 times, the leader can declare "We have all...". This is because each of the 99 other prisoners have turned the switch off exactly once.
If the initial position of the switch is unknown, we cannot use our simple protocol since we may miscount by one. However, we can easily fix the protocol,
by overcompensating this uncertainty of one: We simply let each prisoner turn the switch off twice. Then the leader can safely declare "We have all..." after throwing the switch on 2x99 = 198 times.
|
|
|
|
100 Boxes:
To be released from prison, 100 prisoners have to win a game against the hangman. The names of 100 prisoners are placed in 100 wooden boxes, one name per box, and the boxes are lined up in a room. One by one, the prisoners are led into the room; each may look into at most 61 boxes (61 is the lucky number of the hangman!), but must leave the room exactly as he found it and is permitted no further communication with the others. The prisoners have a chance to plot their strategy in advance. If each and every prisoner finds his name, all prisoners are released. If only one prisoner does not find his name, the hangman executes his job (on all the prisoners). Is it possible to come up with a scheme such that the chance of winning is higher than losing?
|
Hints: As always, you should first think about a simplified version of the game. Here only two prisoners that each check out one of two boxes allows for a simple 50% solution. Generalizing this solution is not really straightforward, however.
For the solution, please hit the puzzle name again.
|
|
|
Solution: With only two prisoners (and boxes), prisoner A should simply check the first box, whereas prisoner B should check the second box. That way they have a 50% chance to survive.
With n prisoners that can open at most k boxes it's more complicated. To solve it, the prisoners must first agree on a random labeling of the boxes by their own names; more concretely, they must all memorize the name of the same random prisoner on the first box, the same random prisoner on the second box, etc. When admitted to the room, each prisoner first inspects his own box (that is, the box with which he has been associated). He then looks into the box associated to the name he just found, etc., until he either finds his own name, or has opened k boxes (and loses). That's the strategy.
Why should it work?! Since the boxes are associated randomly, the first prisoner will find his name with probability 1/n in the first box. His name will be in the second box with probability 1/(n-1). And so on. The probability that he finds his name within k boxes is k/n. Indeed, assume that he finds his name in exactly k steps. This means that all the boxes he checked form a logical cycle. In other words, also all the other prisoners of that cycle will find their name in exactly k steps. Moreover, the other prisoners (not in that cycle) will be in a different cycle of the random permutation. So the question we need to ask is whether a random permutation of n numbers has a cycle of length more than m.
We restrict ourselves to m > n/2, then any permutation can at most have one m-cycle. What's the probability of such an m-cycle? Well, there are (n choose m) ways to pick the entries of the cycle, and (m-1)! Ways to order them. The rest can be permuted in (n-m)! ways. Altogether that's
(n choose m)*(m-1)!*(n-m)! = n!/m
ways to have a cycle of length m. Since there are n! permutations, the probability to have one of exactly length m becomes 1/m. We need to worry about all cycles that are strictly larger than k. The probability to have one is
P = 1-1/(k+1)-1/(k+2)-...-1/n = 1+H(n)-H(k),
where H() is the harmonic series, roughly H(x) = ln x. For n=100 and k=61, we get P = 50.9%. In other words, when following this scheme the prisoners have a higher chance to win than to lose.
There are some nice YouTube videos explaining this phenomenon, for instance by Veritasium.
|
|
|
|
The Village:
Many years ago there was a tiny village, populated with 20 couples. The husbands meet every noon to discuss village matters. The husbands all were horribly jealous. If one ever figures out that his wife ever cheated on him, he will kill himself the following night, at midnight. Obviously, no (living) husband knew whether his wife cheated. Despite all this, gossiping was popular in the village, and every husband knew exactly which wives cheated (apart from his own wife of course). One day an ethnologist came to town. After a few days in the village he announced he was surprised to find cheating (in such a small village). After that the ethnologist left town again. What happened next?
|
Hints: As always, you should first think about a simplified version of the game, with less couples, and a given number of cheaters.
For the solution, please hit the puzzle name again.
|
|
|
Solution: If exactly one wife is cheating her husband will kill himself the following midnight. Why? So far he did not know that there was cheating in the village, and assuming that he has exact knowledge about cheating, he concludes that he must be the cheated one, killing himself.
If two wifes are cheating, nothing happens the first night, as both cheated husbands know one cheating wife, expecting that poor husband to commit suicide the following midnight. However, there is no suicide, so both conclude that there must be at least two cheaters, hence committing suicide the following night.
With three cheating wives it's just one step more. All three husbands assume that the two others commit suicide the second night; if they don't they will commit suicide the third night.
And so on, if there are k cheating wives in the village, the k cheated husbands will commit suicide in night k after the ethnologist left the village.
|
|
|
|
The Number:
You must guess the secret number of a mathematical Rumpelstiltskin. For all statements x below: If statement x is true, then x must be a digit of the secret number; if statement x is false, the digit x must not be in the number. What's the secret number?
1. The product of the digits is odd.
2. Every digit is smaller than the next digit (if available).
3. No two digits are the same.
4. No digit is larger than 4.
5. The number has less than 6 digits.
6. The product of the digits is not divisible by 6.
7. The number is even.
8. No two digits have a difference of 1.
9. We have a = b + c, where a, b, and c are three digits of the number. (If a digit is used twice in the number, we can also use it twice.)
0. This number does not exist!
|
Hints: Try to more or less greedily find the next true of false statement. Since it would be boring if the number didn't exist, let us assume that statement 0 is false, and hence the digit 0 does not appear in the number. Now find the next statement that is definitely true or false!
For the solution, please hit the puzzle name again.
|
|
|
Solution: 0. Let us assume that the number exists, so 0 is not a digit.
6. If 6 was a digit, then the product of digits would be divisible by 6. Hence statement 6 is false, and 6 is not a digit.
1. Let us assume that there is at least one even digit in the number, so 1 is not a digit. (we need another assumption?)
4 not?
8 yes
7 not
9 not
5 in?!?
i can't remember my own solution... :-)
|
|
|
|
The Queue:
100 men stand in a queue, all looking in the same direction. Each man is wearing a hat. Hence, the last man can see all hats but his own, while the first man in the queue cannot see anybody's hat. The hats have a shape of a single digit, from 0 to 9. Starting with the last man in the queue, each man says a single digit, hopefully the digit on its own hat. Show how almost all the men can guess correctly!
|
Hints: It's pretty simple to find a scheme where at least 50 men are guessing right, but maybe you can push your technique even more?
For the solution, please hit the puzzle name again.
|
|
|
Solution: The last man in the queue sums up all the hats, divides the result by 10, and announces the remainder (most probably wrongly!). However, with this information the second last man can figure out its digit: He sums up the values on the 98 hats he can see. Removing this sum from the value he just heard from the last man modulo 10 gives his own hat's digit. All the other men in the queue just keep removing the values from the digit the last men said, and figure out their own digit by looking at the sum in front of them. With that all but the last man will say the correct digit.
|
|
|
|
|
|